Recently, Asia Technology Laboratory is studying solar photovoltaic power generation, and began to think about the installation position and angle of photovoltaic panels:

The best location for the installation of solar photovoltaic should be where the sun can shine at all times. Solar photovoltaic panels can get the maximum light exposure, and there are no buildings, structures and trees around. The best location in and around the city is the open roof.

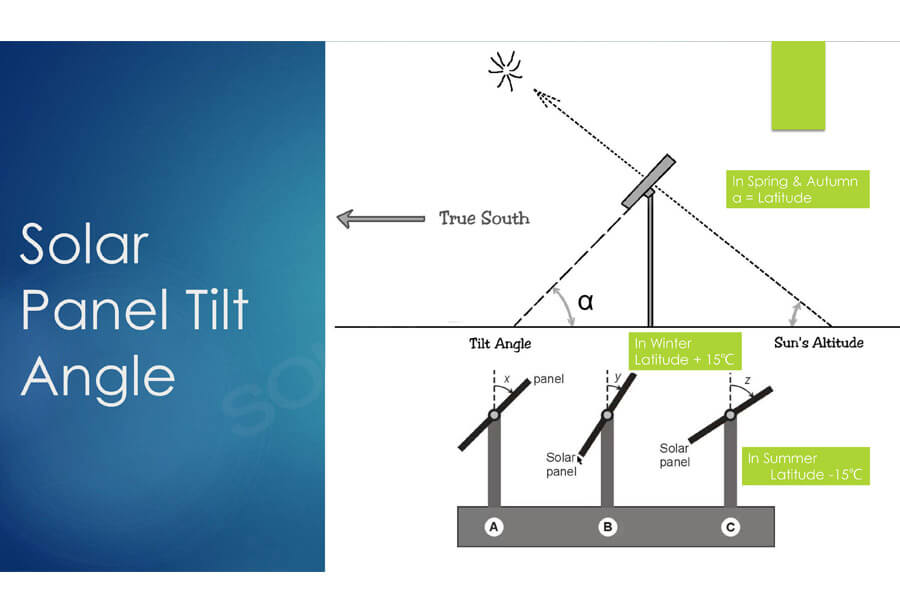
China’s latitude span is large, and the solar altitude (actually the solar altitude angle) is different in different dimensions. The installation angle of photovoltaic panels in different latitudes should be different. Therefore, the installation angle needs to be calculated.

This reminds me of the ancient Chinese timing tool: sundial. The sundial is a round dial with a long compass needle in the middle. It is installed in an open place according to a certain angle. According to the angle of the shadow of the long compass needle in the middle after the sunlight, it can specify the hour or moment at that time. It is a commonly used timing instrument in ancient China.

The center of the sundial face faces due south. At 12 o’clock in the summer solstice, the shadow formed by the long needle of the sundial coincides with itself, which shows that the pitching angles of sundials in different dimensions are different.

The photovoltaic installation should be installed in the due south to ensure the best comprehensive incidence angle from morning to noon to night every day, so it faces the due south.

The installation angle of the pitch of the photovoltaic panel should seek to maximize the annual average incidence angle. The highest efficiency of photovoltaic power generation is to direct the light to the photovoltaic panel as much as possible.

How to calculate the altitude angle of the sun:

If the latitude difference from the direct point of the sun is one degree, the height angle of the noon sun will be reduced by one degree.

From the longitude and latitude of the direct sunlight point to the north and south sides. It can be inferred that the latitude difference from the direct point of the sun is one degree, and the noon solar altitude angle is reduced by one degree. (it can be further concluded that when the height angle of the sun at a certain noon is known, there are generally two latitudes equal to this degree).

For example, when the sun shines directly at 20 ° n, the global noon solar altitude angle gradually decreases from 20 ° n to the north and south sides on that day, and the noon solar altitude angle of 19 ° n is equal to 89 °. That is, the noon solar height of 19 ° n = 90 ° – (direct point of the sun – local latitude) = 90 ° – (20 ° – 19 °) = 89 °

We use h to express this angle, which is numerically equal to the horizontal height of the sun in the celestial horizontal coordinate system.

The solar altitude angle changes with the local time and the declination of the sun. Solar declination (equal to the latitude of the direct point of the sun) δ Indicates the geographic latitude of the observation site φ Indicates (both solar declination and geographical latitude are positive in north latitude and negative in south latitude), local time (time angle) is expressed in T, and there is the calculation formula of solar altitude angle:

sin h= sin φ sin δ+ cos φ cos δ cos t

When the solar altitude angle is 90 °, the solar radiation intensity is the largest; When the sun shines obliquely on the ground, the intensity of solar radiation is small.

For a certain place on the earth, the solar height refers to the angle between the incident direction of sunlight and the ground plane. Solar irradiance is the most important factor that determines the amount of solar thermal energy obtained by the earth’s surface.

At sunrise and sunset, the solar altitude angle changes continuously in the same place in a day. The angles of sunrise and sunset are zero degrees, and the height angle of the sun is the largest.

The noon hour angle is 0, and the above formula can be simplified as:

sinh＝sin φ sin δ＋ cos φ cos δ

Where h is the height angle of the noon sun.

From the trigonometric function formula of sum and difference of two angles

sinh＝cos( φ－δ)

So,

For the northern hemisphere, H = 90 °－（ φ－δ)；

For example:

The position where we install solar photovoltaic panels is 35 ° 25 ′ 828552 ″ north latitude. The height of the sun at noon:

The time of summer solstice is about 90 ° – (35 ° 26 ‘- 23 ° 26’) ≈ 78 °

The solar altitude angle of the winter solstice is about 90 ° – (35 ° 26 ‘+ 23 ° 26’) ≈ 32 ° 8 ‘

Calculate the best angle of photovoltaic panel installation:

（（90°-78°）+（90°-32°8′））/2≈35°

Therefore, the best angle for local photovoltaic installation is about 35 degrees.