Due to the fact that solar energy is a clean energy source, its application is rapidly growing worldwide. Using solar energy for power generation is a way of using solar energy, but currently the cost of building a solar power generation system is still relatively high. From the current cost of solar power generation in China, the cost of solar cell components is about 30-40%.

Therefore, in order to make more full and effective use of solar energy, how to select the azimuth and tilt angles of the solar cell array is a very important issue.

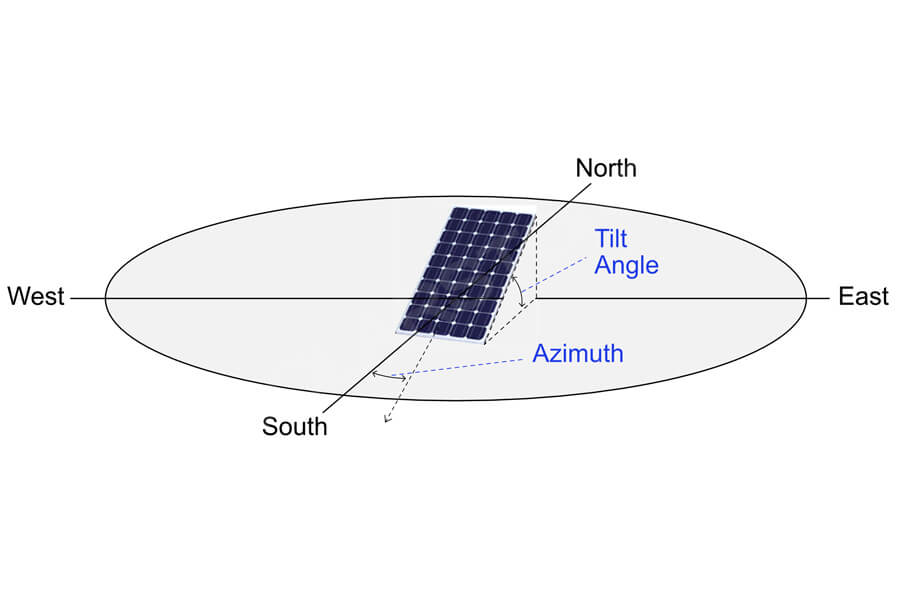
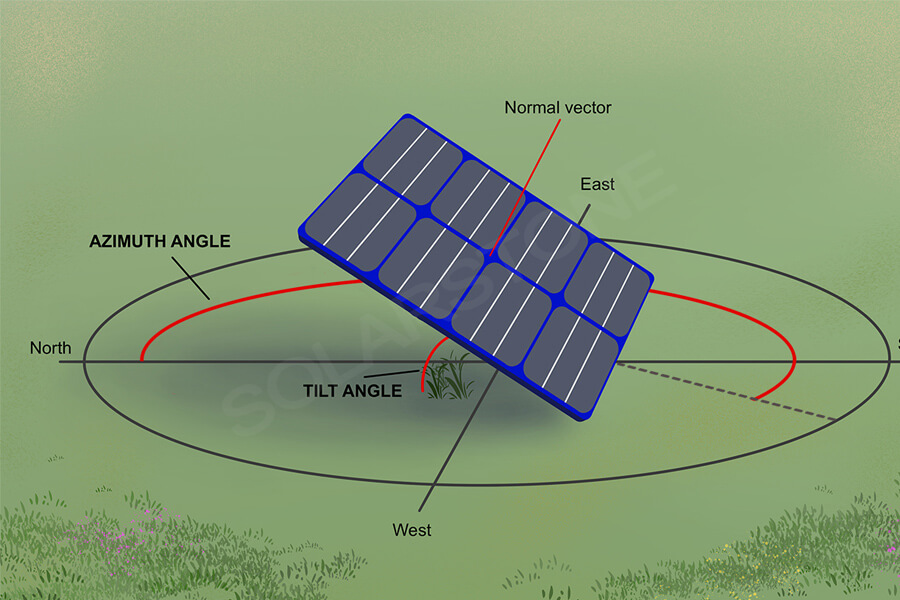
1. Azimuth angle

The azimuth angle of a solar cell array is the angle between the vertical plane of the array and the south direction (set as negative angle for eastward deviation and positive angle for westward deviation).

In general, when the square array faces due south (i.e. the angle between the vertical plane of the square array and due south is 0 °), the solar cell power generation is maximum.

When deviating from the due south (northern hemisphere) by 30 degrees, the power generation of the square array will decrease by about 10% to 15%; When deviating from the due south (northern hemisphere) by 60 °, the power generation of the square array will decrease by about 20% to 30%.

However, in clear summer, the maximum moment of solar radiation energy occurs later in the afternoon, so when the direction of the array is slightly westward, the maximum power generation can be obtained in the afternoon. In different seasons, when the orientation of the solar cell array is slightly east or west, the maximum power generation can be achieved.

The location of the square array is constrained by many conditions, such as the azimuth angle of the land when set on the ground, the azimuth angle of the roof when set on the roof, or the azimuth angle when set to avoid the shadow of the sun, as well as many factors such as layout planning, power generation efficiency, design planning, and construction purposes.

If you want to adjust the azimuth angle to match the peak load moment and the peak power generation moment in a day, please refer to the following formula. Azimuth angle=(peak time of load in a day (24-hour system) -12) x 15+(longitude -116)

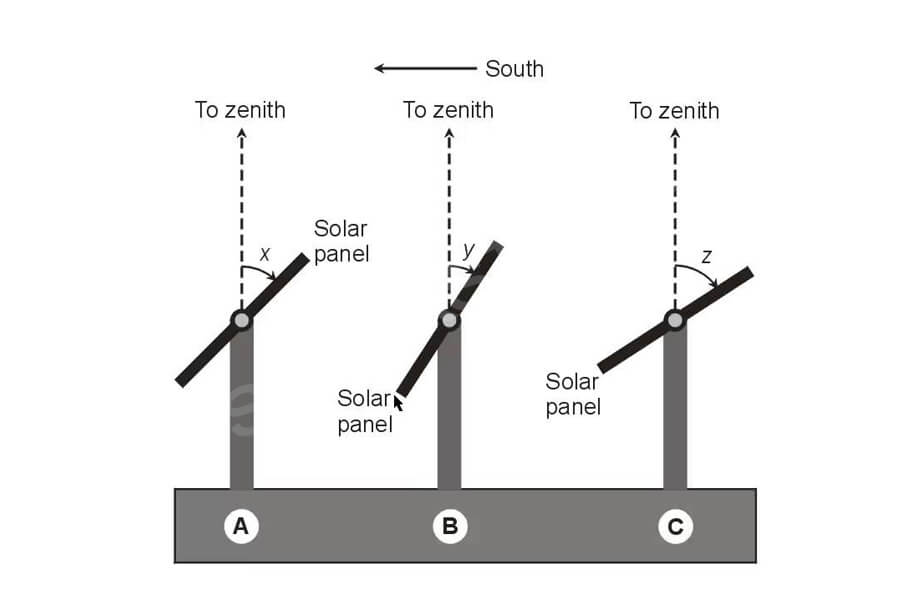
2. Tilt angle

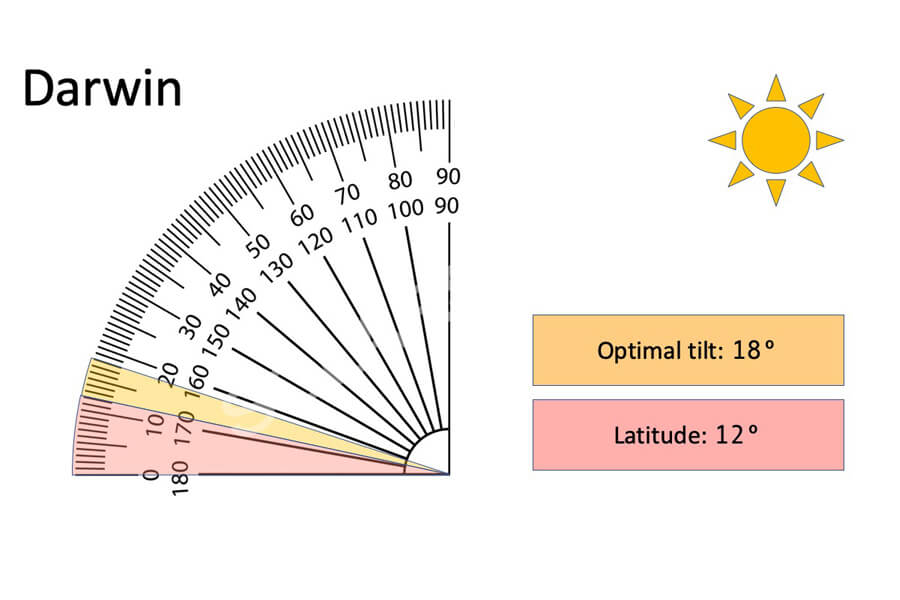
The tilt angle is the angle between the plane of the solar cell array and the horizontal ground, and it is hoped that this angle is the optimal tilt angle for the array when its annual power generation is at its maximum. The optimal tilt angle of the year is related to the local geographic latitude, and when the latitude is higher, the corresponding tilt angle is also larger.

However, like azimuth, the design also needs to consider limitations such as the inclination angle of the roof and the inclination angle of snow sliding (with a slope greater than 50% -60%). For the inclination angle of snow sliding, even during the snow covered period, there is an increase in annual total power generation despite a decrease in power generation.

Therefore, especially in grid connected power generation systems, the sliding of snow may not necessarily be given priority, and other factors need to be further considered.

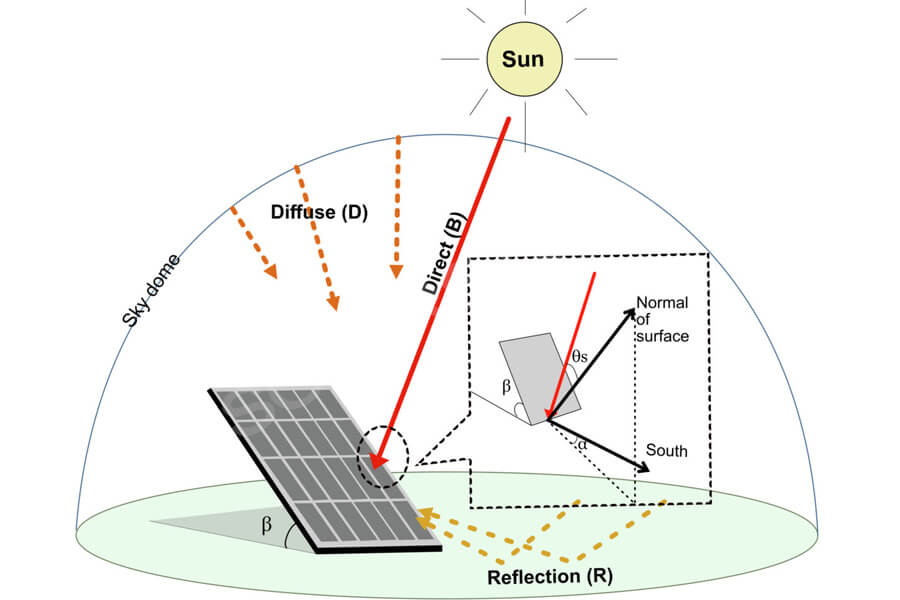
For due south (with an azimuth angle of 0 °), as the tilt angle gradually transitions from horizontal (with an inclination angle of 0 °) to the optimal tilt angle, the amount of solar radiation continuously increases until it reaches its maximum value, and then decreases as the tilt angle increases.

Especially after the inclination angle is greater than 50 ° to 60 °, the solar radiation sharply decreases until the final vertical placement, when the power generation decreases to the minimum. There are practical examples of square arrays being placed vertically and tilted from 10 ° to 20 °.

For cases where the azimuth angle is not 0 °, the value of oblique solar radiation is generally low, and the maximum solar radiation value is near the inclination angle close to the horizontal plane. The above is the relationship between azimuth angle, tilt angle and power generation. For the specific design of a square array, the azimuth angle and tilt angle should be further considered in combination with the actual situation.

3. The impact of shadows on power generation

In general, when calculating power generation, we obtain it on the premise that there are no shadows on the square array. Therefore, if the solar cell cannot be directly illuminated by sunlight, then only scattered light is used to generate electricity, and the power generation at this time is reduced by about 10% to 20% compared to shadowless ones.

In response to this situation, we need to correct the theoretical calculated values. Usually, when there are buildings and peaks around the square array, there will be shadows around the buildings and mountains after the sun comes out.

Therefore, when choosing the location for laying the square array, it is advisable to avoid shadows as much as possible. If it is really impossible to avoid it, the wiring method of the solar cell should also be solved to minimize the impact of shadows on power generation.

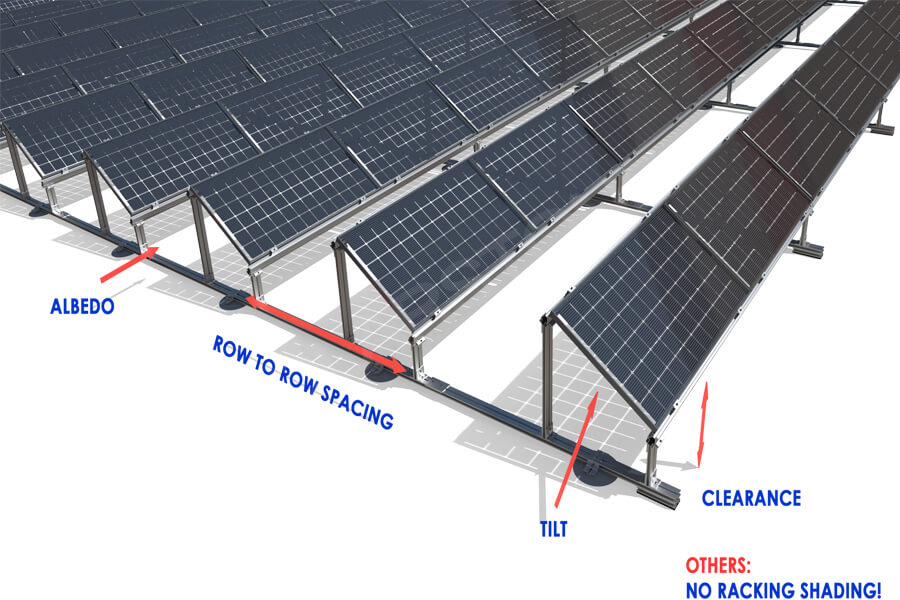
In addition, if the square array is placed in front and back, and the distance between the rear square array and the front square array is close, the shadow of the front square array will have an impact on the power generation of the rear square array.

There is a bamboo pole with a height of L1, and its shadow length in the north-south direction is L2. The sun’s height (elevation) is A, and when the azimuth is B, assuming the magnification of the shadow is R, then:

R=L2/L1=ctgA x cosB

This formula should be calculated based on the day of the winter solstice.

Because that day had the longest shadow. For example, if the height of the upper edge of a matrix is h1 and the height of the lower edge is h2, then the distance between the matrices a=(h1-h2) x R. When the latitude is higher, the distance between the squares increases, and the corresponding area of the set location will also increase.

For square arrays with anti snow measures, their tilt angle is large, which increases the height of the arrays. To avoid the influence of shadows, the distance between the arrays will also increase accordingly.

Usually, when arranging a square array, the construction size of each square array should be selected separately, and its height should be adjusted to an appropriate value, so as to use its height difference to minimize the distance between the squares.

The specific design of solar cell arrays should not only reasonably determine the azimuth and tilt angles, but also comprehensively consider them in order to achieve the optimal state of the array.